from simplextree import SimplexTree
st = SimplexTree([[1,2,3],[2,3,4,5],[6,7,9],[7,8],[10]]) # complex form the picture
print(st)Simplex Tree with (10, 12, 6, 1) (0, 1, 2, 3)-simplicesOverview of the simplextree package
A simplicial complex S is a pair S = (V, \Sigma) where V is a vertex set and \Sigma \subseteq \mathcal{P}(V) is a collection of simplices satisfying:
- If v \in V, then \{v\} \in \Sigma
- If \tau \subset \sigma for some \sigma \in \Sigma, then \tau \in \Sigma
Simplicial complexes generalize graphs. Like graphs, there are many ways to represent simplicial complexes in memory. One such way is to use a Simplex Tree: an ordered, trie-like structure whose nodes are in bijection with the faces of the complex. Here’s a picture of a simplicial 3-complex (left) and its corresponding Simplex Tree (right):
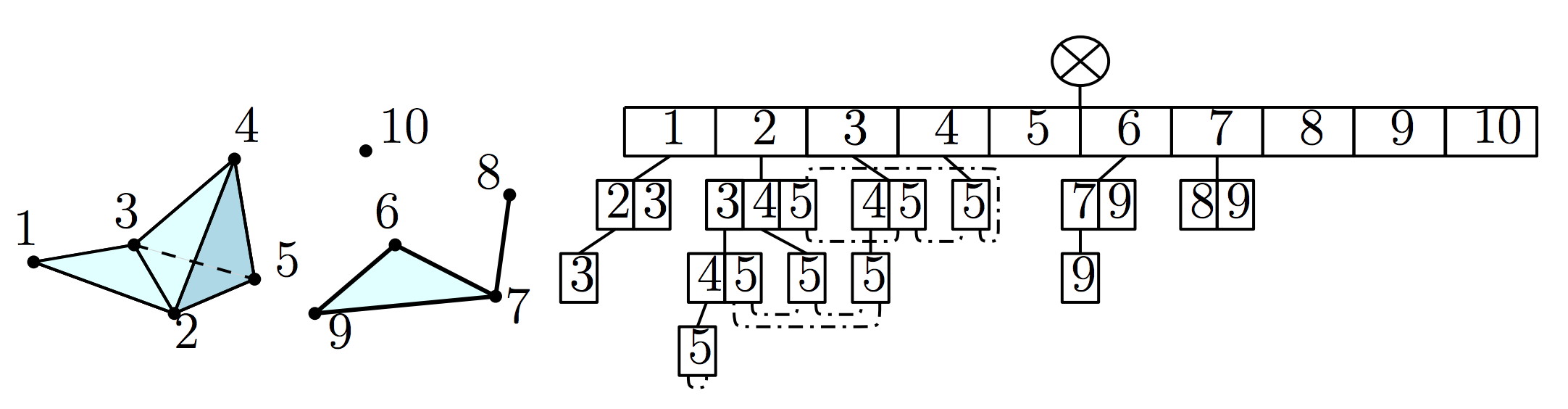
To construct the complex above with a simplextree package, simply give the maximal simplices:
To look at the tree structure, use print_tree (see also: print_cousins)
st.print_tree()1 (h = 2): .( 2 3 )..( 3 )
2 (h = 3): .( 3 4 5 )..( 4 5 5 )...( 5 )
3 (h = 2): .( 4 5 )..( 5 )
4 (h = 1): .( 5 )
5 (h = 0):
6 (h = 2): .( 7 9 )..( 9 )
7 (h = 1): .( 8 9 )
8 (h = 0):
9 (h = 0):
10 (h = 0): To maintain fast coface lookup and enumeration, extra links are added between nodes at the same level, which are shown by the dash-dotted lines in the figure above (only for the nodes with the label 5). To view these links with the SimplexTree class, use print_cousins():
st.print_cousins()(last=2, depth=2): { 1 2 }
(last=3, depth=2): { 1 3 } { 2 3 }
(last=4, depth=2): { 2 4 } { 3 4 }
(last=5, depth=2): { 2 5 } { 3 5 } { 4 5 }
(last=7, depth=2): { 6 7 }
(last=8, depth=2): { 7 8 }
(last=9, depth=2): { 6 9 } { 7 9 }
(last=3, depth=3): { 1 2 3 }
(last=4, depth=3): { 2 3 4 }
(last=5, depth=3): { 2 3 5 } { 2 4 5 } { 3 4 5 }
(last=9, depth=3): { 6 7 9 }
(last=5, depth=4): { 2 3 4 5 }