Research Projects
Spectral relaxations of persistent rank invariants
TopologyPersistenceLinear AlgebraWe introduce a framework for constructing families of continuous relaxations of the persistent rank invariant for persistence modules indexed over the real line. Applications to multi-parameter persistence, parameter optimization, and shape classification are also presented.
Using the fact that the persistent rank invariant determines the persistence diagram and vice versa, we introduce a framework for constructing families of continuous relaxations of the persistent rank invariant for persistence modules indexed over the real line. Like the rank invariant, these families obey inclusion-exclusion, are derived from simplicial boundary operators, and encode all the information needed to construct a persistence diagram. Unlike the rank invariant, these spectrally-derived families enjoy a number of stability and continuity properties typically reserved for persistence diagrams, such as smoothness and differentiability over the positive semi-definite cone. By leveraging its relationship with combinatorial Laplacian operators, we find the non-harmonic spectra of our proposed relaxation encode valuable geometric information about the underlying space, prompting several avenues for geometric data analysis. As these Laplacian operators are trace-class operators, we also find the corresponding relaxation can be efficiently approximated with a randomized algorithm based on the stochastic Lanczos quadrature method. We investigate the utility of our relaxation with applications in topological data analysis and machine learning, such as parameter optimization and shape classification. Publications
- Piekenbrock, Matthew, and Jose A. Perea. “Spectral families of persistent rank invariants.” Computational Persistence Workshop (2023). (link)
Software
- pbsig unorganized code containing the experiments
- primate package code for implicit matrix trace estimation
- simplextree (python package)
Related materials
- YouTube link for CompPers23 talk
Move Schedules: Fast persistence computations in coarse dynamic settings
TopologyAlgorithmsPersistencePersistence diagrams are known to vary continuously with respect to their input, motivating the study of their computation for time-varying filtered complexes. Computationally, simulating persistence dynamically can be reduced to maintaining a valid decomposition under adjacent transpositions in the filtration order. Since there are quadratically many such transpositions, this maintenance procedure exhibits limited scalability and often is too fine for many applications. We propose a coarser strategy for maintaining the decomposition over a 1-parameter family of filtrations that requires only subquadratic time and linear space to construct.

Matrix reduction is the standard procedure for computing the persistent homology of a filtered simplicial complex with $m$ simplices. Its output is a particular decomposition of the total boundary matrix, from which the persistence diagrams and generating cycles are derived. Persistence diagrams are known to vary continuously with respect to their input, motivating the study of their computation for time-varying filtered complexes. Computationally, simulating persistence dynamically can be reduced to maintaining a valid decomposition under adjacent transpositions in the filtration order. Since there are quadratically such transpositions, this maintenance procedure exhibits limited scalability and often is too fine for many applications. We propose a coarser strategy for maintaining the decomposition over a 1-parameter family of filtrations that requires only superlinear time and linear space to construct. By reduction to a particular longest common subsequence problem, we show the storage needed to employ this strategy is actually sublinear in expectation. Exploiting this connection, we show experimentally that the decrease in operations to compute diagrams across a family of filtrations, is proportional to the difference between the expected quadratic number of states and the proposed sublinear coarsening. Applications to video data, dynamic metric space data, and multi-parameter persistence are also presented. Publications
- Piekenbrock, Matthew, and Jose A. Perea. “Move Schedules: Fast persistence computations in coarse dynamic settings.” arXiv preprint arXiv:2104.12285 (2021).
Software
- Move scheduling code
- simplextree (python package)
Efficient Multiscale Simplicial Complex Generation for Mapper
ClusteringTopologyR PackageThe primary result of the Mapper framework is the geometric realization of a simplicial complex, depicting topological relationships and structures suitable for visualizing, analyzing, and comparing high dimensional data...
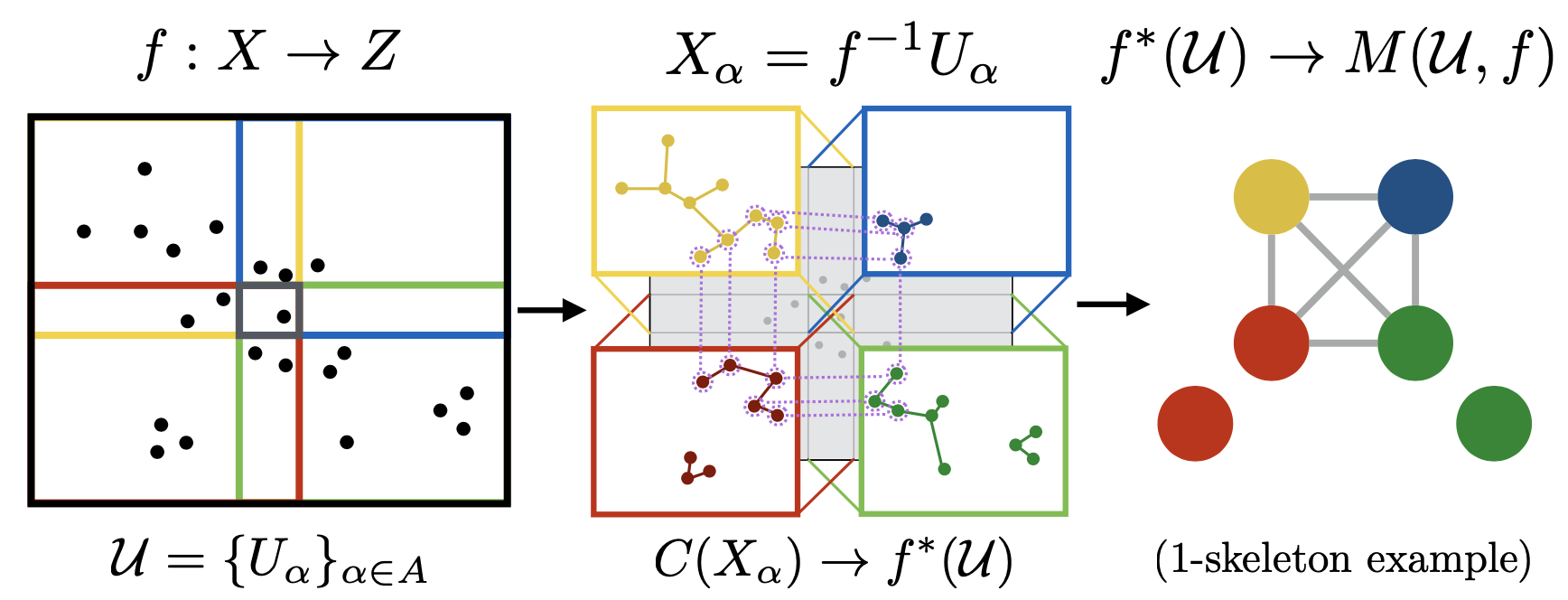
The primary result of the Mapper framework is the geometric realization of a simplicial complex, depicting topological relationships and structures suitable for visualizing, analyzing, and comparing high dimensional data. As an unsupervised tool that may be used for exploring or modeling heterogeneous types of data, Mapper naturally relies on a number of parameters which explicitly control the quality of the resulting construction; one such critical parameter controls the entire relational component of the output complex. In practice, there is little guidance on what values may provide 'better' or more 'stable' sets of simplices. In this effort, we provide a new algorithm that enables efficient computation of successive mapper realizations with respect to this crucial parameter. Our results not only enhances the exploratory/confirmatory aspect of Mapper, but also give tractability to recent theoretical extensions to Mapper related to persistence and stability. Publications
- Multiscale Mapper paper (never finished!)
Software
- Mapper (R Package)
- simplextree (R Package)
- Vignette on using Mapper for shape recognition
Automating Point of Interest Discovery in Geospatial Contexts
ClusteringGeospatial analysisNetwork modelingWith the rapid development and widespread deployment of sensors dedicated to location-acquisition, new types of models have emerged to predict macroscopic patterns that manifest in large data sets representing "significant" group behavior. Partially due to the immense scale of geospatial data, current approaches to discover these macroscopic patterns are primarily driven by inherently heuristic detection methods. Although useful in practice, the inductive bias adopted by such mainstream detection schemes is often unstated or simply unknown. Inspired by recent theoretical advances in efficient non-parametric density level set estimation techniques, in this research effort we describe a semi-supervised framework for automating point of interest discovery in geospatial contexts. We outline the flexibility and utility of our approach through numerous examples, and give a systematic framework for incorporating semisupervised information while retaining finite-sample estimation guarantees.

With the rapid development and widespread deployment of sensors dedicated to location-acquisition, new types of models have emerged to predict macroscopic patterns that manifest in large data sets representing "significant" group behavior. Partially due to the immense scale of geospatial data, current approaches to discover these macroscopic patterns are primarily driven by inherently heuristic detection methods. Although useful in practice, the inductive bias adopted by such mainstream detection schemes is often unstated or simply unknown. Inspired by recent theoretical advances in efficient non-parametric density level set estimation techniques, in this research effort we describe a semi-supervised framework for automating point of interest discovery in geospatial contexts. We outline the flexibility and utility of our approach through numerous examples, and give a systematic framework for incorporating semisupervised information while retaining finite-sample estimation guarantees. Publications
- Piekenbrock, Matthew J. Discovering Intrinsic Points of Interest from Spatial Trajectory Data Sources. Masters thesis. Wright State University, 2018. link
- Piekenbrock, Matthew, and Derek Doran. “Intrinsic point of interest discovery from trajectory data.” arXiv:1712.05247 (2017) (doi: https://doi.org/10.48550/arXiv.1712.05247)
- Matthew Maurice, Matt Piekenbrock, and Derek Doran. Waminet: An open source library for dynamic geospace analysis using WAMI. In IEEE International Symposium on Multimedia, pages 445–448. IEEE, 2015.
Bringing High Performance Density-based Clustering to R
ClusteringR PackageHigh performance computingDensity-based clustering techniques have become extremely popular in the past decade. It's often conjectured that the reason for the success of these methods is due to their ability of identify 'natural groups' in data. These groups are often non-convex (in terms of shape), deviating the typical premise of 'minimal variance' that underlies parametric, model-based approaches, and often appear in very large data sets. As the era of 'Big Data' continues to rise in popularity, it seems that typical notions having access to scalable, easy-to-use, and scalable implementations of these density-based methods is paramount. In this research effort, we provide fast, state-of-the-art density-based algorithms in the form of an open-source package in R. We also provide several related density-based clustering tools to help bring make state of the art density-based clustering accessible to people with large, computationally difficult problems.
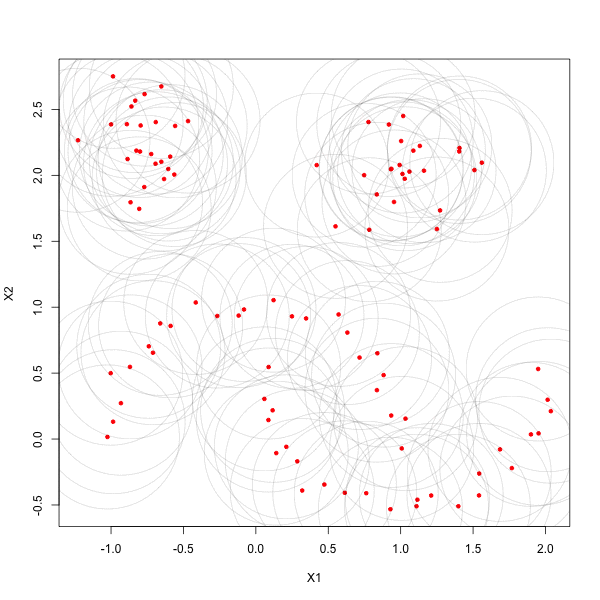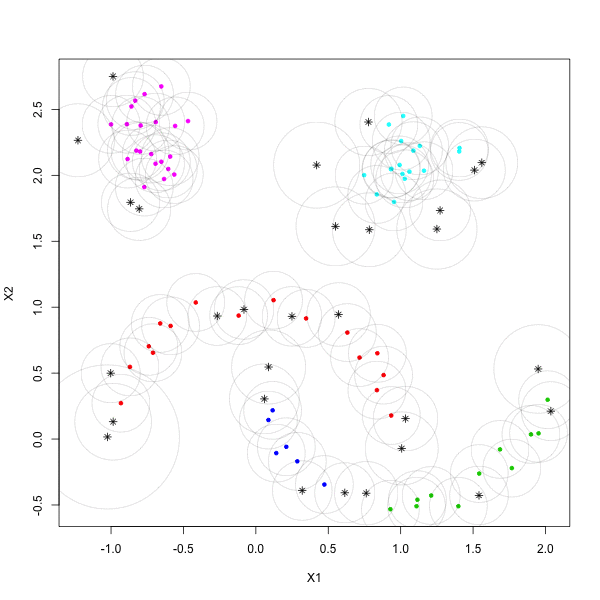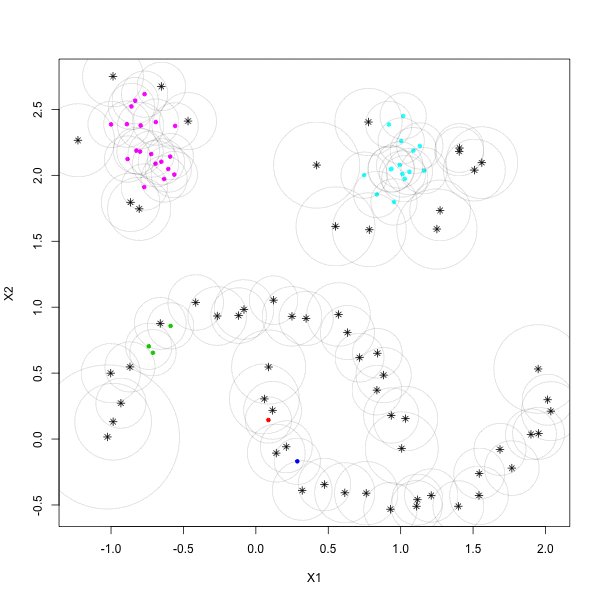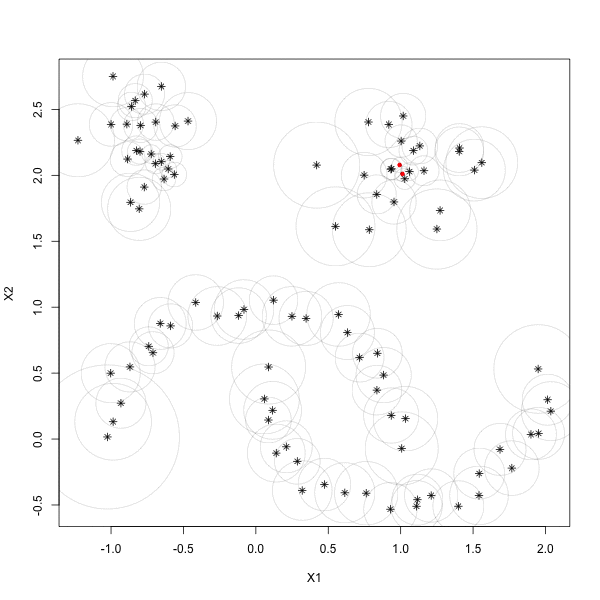
Density-based clustering techniques have become extremely popular in the past decade. It's often conjectured that the reason for the success of these methods is due to their ability of identify 'natural groups' in data. These groups are often non-convex (in terms of shape), deviating the typical premise of 'minimal variance' that underlies parametric, model-based approaches, and often appear in very large data sets. As the era of 'Big Data' continues to rise in popularity, it seems that typical notions having access to scalable, easy-to-use, and scalable implementations of these density-based methods is paramount. In this research effort, we provide fast, state-of-the-art density-based algorithms in the form of an open-source package in R. We also provide several related density-based clustering tools to help bring make state of the art density-based clustering accessible to people with large, computationally difficult problems. Publications
- Hahsler, Michael, Matthew Piekenbrock, and Derek Doran. “dbscan: Fast Density Based Clustering in R”, Journal of Statistical Software, 2018. (https://doi.org/10.18637/jss.v091.i01)
Software
- dbscan (R Package)
- Vignette on using HDBSCAN
Towards Autonomous Aerial Refueling: Massive Parallel Iterative Closest Point
GeometryPoint registrationHigh performance computingThe Iterative Closest Point (ICP) problem is now a well-studied problem that seeks to align a given query point cloud to a fixed reference point cloud. The ICP problem computationally is dominated by the first phase, a pairwise distance minimization. The ''brute-force'' approach, an embarrassingly parallel problem amenable to GPU-acceleration..

The Iterative Closest Point (ICP) problem is now a well-studied problem that seeks to align a given query point cloud to a fixed reference point cloud. The ICP problem computationally is dominated by the first phase, a pairwise distance minimization. The 'brute-force' approach, an embarrassingly parallel problem amenable to GPU-acceleration, involves calculating the pairwise distance from every point in the query set to every point in the reference set. This however still requires linear runtime complexity per thread, rendering the trivial solution unsuitable for e.g. real-time applications. Alternative spatial indexing data structures utilizing branch-and-bound (B&B) properties have been proposed as a means of reducing the algorithmic complexity of the ICP problem, however they were originally developed for serial applications: it is well known that direct conversion to their parallel equivalents often results in slower runtime performance than GPU-employed brute-force approaches due to frequent suboptimal memory access patterns and conditional computations. In this application-motivated effort, we propose a novel two-step method which exposes the intrinsic parallelism of the ICP problem, yet retains a number of the B&B properties. Our solution involves an O(log n) approximate search, followed by fast vectorized search we call the Delaunay Traversal, which we show empirically finishes in O(k) time on average, where k << n, and is demonstrated to generally exhibit extremely small growth factors on average. We demonstrate the superiority of our method compared to the traditional B&B and brute-force implementations using a variety of benchmark data sets, and demonstrate its usefulness in the context of Autonomous Aerial Refueling Publications
- J. Robinson, M. Piekenbrock, L. Burchett, et. al. Parallelized Iterative Closest Point for Autonomous Aerial Refueling. In International Symposium on Visual Computing (pp. 593-602). Springer International Publishing. (2016, December) (doi: 10.1007/978-3-319-50835-1_53)
- Piekenbrock, M., Robinson, J., Burchett, L., Nykl, S., Woolley, B., & Terzuoli, A. (2016, July). Automated aerial refueling: Parallelized 3D iterative closest point: Subject area: Guidance and control. In Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS), 2016 IEEE National (pp. 188-192). IEEE. (doi: 10.1109/NAECON.2016.7856797)
